Table of Contents
Überholabstand aus mathematischer Perspektive
Die Vorgeschichte
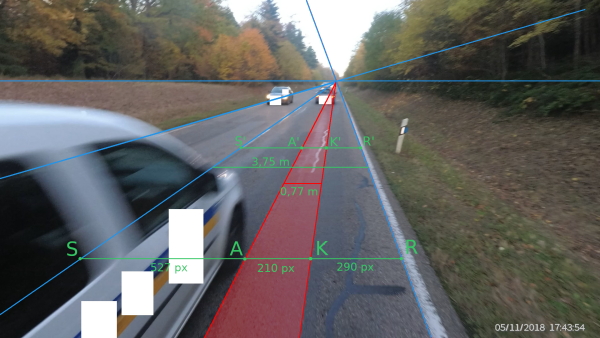
Wer mit dem Fahrrad unterwegs ist, nimmt den Straßenverkehr oftmals anders wahr. Entsprechende Infrastruktur vorausgesetzt fährt man mit dem Rad einfach am Autostau vorbei. Manchmal aber teilt man sich die Straße und muss mit einer besonderen Spezies, dem Autofahrensis Überholis, Bekanntschaft machen. Diese Spezies zeichnet sich durch eine räumliche Wahrnehmung aus, die sich sehr von der des Gemeinen Radfahrers unterscheidet. Manch ein Exemplar des Gemeinen Radfahrers rüstet technisch auf, befestigt Action-Kameras an seinem Rad und zeichnet potenzielle Gefahrensituationen auf, um für den Fall der Fälle gewappnet zu sein, den knappen Überholvorgang durch einen besonders motivierten Autofahrensis Überholis. Am heimischen Computer sieht das dann so aus:
„Das war wirklich gefährlich! Fast hätte mich das Auto erwischt! Ich gebe eine Anzeige bei der Polizei auf“, sagt sich der Gemeine Radfahrer und schreitet zur Tat. Auf der Polizeiwache angekommen, sagt man ihm jedoch, dass seine „Beweisfotos“ nicht brauchbar seien, da man dort den vorgeschriebenen Abstand von mindestens 1,50 m nicht einschätzen könne.
Und nun?
Hier kommt die Mathematik ins Spiel, aber zunächst ein paar Beobachtungen:
- Die Straße scheint auf einen einzelnen Punkt zuzulaufen, den sogenannten Fluchtpunkt.
- Teilt man das Foto durch eine senkrechte Linie in eine linke und eine rechte Hälfte, so erhält man die Position der Kamera.
- Eine gedachte Linie von der unteren Mitte zum Fluchtpunkt beschreibt den Weg des Fahrrads, wenn es seine Fahrt im gleichen Abstand vom Fahrbahnrand fortsetzt.
- Genauso kann man den Weg des Autofahrensis Überholis in Richtung Fluchtpunkt vorhersagen, wenn er seine Fahrt im gleichen Abstand fortsetzt.
Wie Geometrie und Dreisatz helfen
Zeichnet man noch ein paar Hilfslinien ein und haut mit dem Mathematik-Hammer einmal fest auf das Foto, so erhält man das folgende Bild:
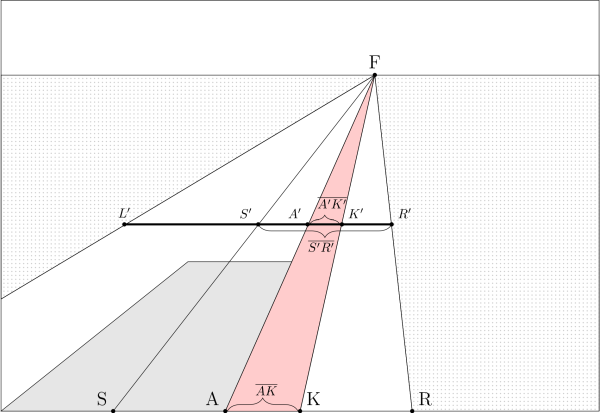
bzw. die folgende abstrakte geometrische Darstellung:
Zwar ist im Vordergrund der linke Fahrbahnrand und die Spurbegrenzung in der Mitte der Fahrbahn durch das Auto verdeckt, aber im Hintergrund sehen wir beides. Mithilfe einer waagerechten Hilfslinie von der Spurmitte zum rechten Fahrbahnrand können wir den Überholabstand bestimmen, sofern die Kamera waagerecht ausgerichtet war und die Breite der Fahrspur bekannt ist (z.B. mind. 3,75 m auf Landstraßen). Vom Fluchtpunkt ausgehend führen weitere Hilfslinien am rechten Fahrbahnrand und der Spurmitte entlang sowie zur Beifahrertür des Autos und zur Mitte des unteren Randes des Fotos (d.h. zur Position der Kamera).
Im Hintergrund sind nun weitere Schnittpunkte entstanden, S' (wie Spurmitte), A' (wie Autotür), K' (wie Kamera) und R' (wie rechter Fahrbahnrand). Weiter unten auf dem Foto haben wir eine parallele Linie gezogen und die entsprechenden Schnittpunkte mit S, A, K und R bezeichnet. Dank des Strahlensatzes ist insbesondere das Längenverhältnis zwischen den Strecken A'K' und S'R' identisch zum Längenverhältnis zwischen den Strecken AK und SR. Als „Formel“ ausgedrückt: $$\frac{A'K'}{S'R'} = \frac{AK}{SR}.$$
Wie misst man diese Strecken auf dem Foto? Die einfachste Lösung ist das Zählen von Pixeln. Man erhält $$SA = 527, \quad AK = 210, \quad KR = 290$$ und somit $$SR = 927.$$ Bei einer tatsächlichen Spurbreite von 3,75 m auf der Landstraße entsprechen also 927 Pixel einer echten Länge von 3,75 m. Wie lang ist die Strecke $AK$ in Wirklichkeit? Dreisatz gibt uns die Antwort: $$ 3,75\,\text{m} \cdot \frac{AK}{SR} = 3,75\,\text{m} \cdot \frac{210}{927} \approx 0,77\,\text{m}.$$
Zum Zeitpunkt des Überholens liegen also 77 Zentimeter zwischen der Kamera und der rechten Tür des Autos. Der tatsächliche Abstand zwischen Fahrrad und Auto ist allerdings noch geringer: Der rechte Seitenspiegel des Autos ragt noch in die rote Zone hinein und links von der Kamera befindet sich in der Regel noch ein gutes Stück Lenker. Angenommen, der Spiegel verschlingt 10 cm und die Kamera ist mittig auf einem 70 cm breiten Lenker befestigt, dann bleiben gerade einmal 32 cm Abstand zwischen Auto und Fahrrad, also viel zu wenig!
Fazit
Es ist möglich, aus einem Foto den Überholabstand zu ermitteln, wenn die Fahrbahnbreite als Referenz bekannt ist und die Kamera waagerecht ausgerichtet ist (d.h. der gedachte Horizont ist ebenfalls waagerecht). Sollte dies nicht der Fall sein, muss das Foto zunächst um den passenden Winkel gedreht werden.